Black on roll owning a 2-cube, leading 11-3 in a 15-point match.

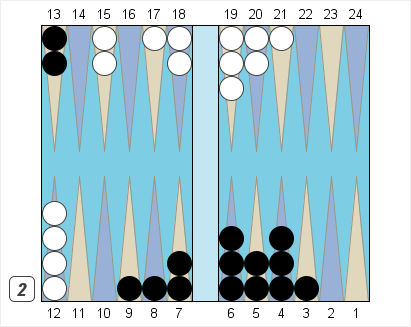Black’s Pip Count = 100

You’re playing a 15-point match, and you’ve got a very comfortable lead, 11-3. You were doubled to two early on, and you took. Now you’ve broken contact, and you’ve got a big lead in the race, 26 pips.

You’d like to redouble, but you don’t know exactly when it’s right to do so. Clearly it’s right at some point, but – are you there yet?

These sorts of problems arise all the time in match play. Most players have a lot of difficulty with them, primarily because our experience with backgammon doubles and takes comes from money play, where all doubles and takes cluster around the 75% range. The doubler wants to be close to a 75% favorite before he doubles, and the taker needs to be about 25% to take. So we know a lot about what 3-to-1 advantages look like, but not much about what 5-to-1 or 8-to-1 or 20-to-1 advantages look like.

Solving positions like this over the board requires three steps:

Step 1: Figure out what the doubling window at this score looks like.

Step 2: Estimate your cubeless winning chances in the position.

Step 3: Compare Step 1 and Step 2.

If you’re inside the window, you should double and your opponent should take (but you’re happy if he drops). If you’re outside the window, either you shouldn’t be doubling or he should be passing. These problems aren’t as difficult to solve as it might seem, once you know the technique plus a couple of tables and rules.

First, let’s figure out what the doubling window is at this score and cube level. We’ll start by calculating the top end of the window – the end corresponding to White’s take point. If White drops, he trails 13-3 in a 15-point match. We can consult match equity tables to get the answer here. Oddly enough, tables from vastly different eras give almost exactly the same answer! Kit Woolsey’s table from 1992 (calculated by hand and published in How to Play Tournament Backgammon) gives the leader a 95% chance of winning at this score. Extreme Gammon’s latest table (based upon bot versus bot results) puts it at 95.25%, a tiny change. Let’s take 95% for easier calculations, meaning White has just 5% chances if he drops the double. If he takes, he can rewhip to 8 and reach 11-11 when he wins, where he’ll win the match half the time. So taking with a 10% chance of winning the game (cubeless) will also give him 5% match winning chances, and therefore the top end of the doubling window is reached when Black is a 90-to-10 favorite in the game.

Our next job is to estimate the other end of the doubling window – the point at which doubling becomes more profitable for Black than waiting. This part is a little tricky. It depends partly on the volatility of the position, which we can’t really quantify well over the board. If we’re willing to settle for a good approximation (which we should in practical play) then we’ll estimate the low end by comparing Black’s gain when he doubles and wins to his loss when he doubles and loses. Here’s how this goes.

Black’s gain when he doubles and wins. If Black doesn’t double and wins, he takes a 13-3 lead, with 95% winning chances (see above). If he doubles and wins, he wins the match. So his gain from doubling and winning is 5%.

Black’s loss when he doubles and loses. If Black doesn’t double and loses, his lead is cut to 11-5. Both Woolsey’s table and XG’s match equity table give about 83% for an 11-5 lead to 15. If Black loses after doubling, the cube will be at 8, since White will automatically rewhip, and the score will be tied 11-11, so Black’s chances will be 50%. The loss from doubling and losing is therefore 83% – 50%, or 33%.

In order to profitably risk 33% to win 5%, you have to be at least a 33/(33+5) = 33/38 = 87% favorite in the position.

So now we have our approximation for the doubling window: 87% to 90%. Black shouldn’t double if his cubeless chances are less than 87%, and White should be passing if Black’s chances are above 90%. Between 87% and 90%, Black should double and White should take.

That’s all well and good, but what’s going on in our actual race position? Black’s pip count is 100, White’s is 126. Black leads by 26%. That’s way more than he needs to cash for money, but how do we know whether he’s 90% or not?

Take a look at the following table. For tournament players, where these sorts of problems arise with some frequency, it’s a good little table to commit to memory:

Leader’s Cubeless Chances Based upon His % Lead in Long Race

10% lead = 75% Cubeless Winning Chances
14% lead = 80% CWC
18% lead = 85% CWC
24% lead = 90% CWC
30% lead = 95% CWC

It’s not a hard table to remember. If you want to make it even easier, note that moving from a 10% race lead to a 30% race lead takes you from 75% winning chances to 95% winning chances. In other words, each extra % of lead translates almost exactly into an extra 1% cubeless winning chances. That lets us create a nice little rule for converting a percentage lead in a race to cubeless winning chances:

Take your percentage lead in the race and add 65 to get your cubeless winning chances.

I call this the Rule of 65, and it’s very useful in many tournament racing positions.

The rule works best for races in the neighborhood of 85 to 115 pips, which covers most interesting non-contact positions with checkers still in the outer boards. For shorter races, you’ll need a slightly larger percentage lead to get to 90% or 95% winning chances. For longer races, a slightly smaller percentage lead will do.

By memorizing this table, problems like this become easy. Black has a 100 to 126 lead, or 26%. Add 65 to that and we get 91% for his cubeless winning chances. (We care only about cubeless winning chances since White’s redouble is forced, after which the cube is dead.) That’s outside the doubling window, so Black should double and White should pass.

In general, the Rule of 65 will give you an answer that’s correct to within 1%, good enough for practical purposes.

Solution: Black should double and White should pass.