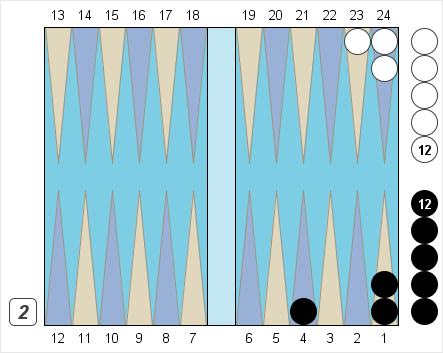
Black – Pips 6 (+2), Match -3 -7
Black on roll. Cube action?
Black leads 4-0 in a 7-point match and owns a 2-cube.
(a) Assume you are Black, you are a very strong player, and you are playing another very strong player. Should Black double in this position? If Black doubles, should White take or drop?
(b) Same question, but now you are Black playing a weak player.
We’ll start by figuring out the correct cube action assuming you and your opponent will make correct decisions in the future. Then we can see if the theoretically correct action requires any adjustment depending on the strength of your opponent.
To figure out the right cube action, we need to estimate three numbers:
(1) Black’s actual chance of winning the game from this point, disregarding the cube.
(2) The value of a 6-0 lead in a 7-point match (which happens if Black doubles to 4 and White drops, or Black doesn’t double and simply wins the game with the cube on 2.)
(3) The value of a 4-2 lead in a 7-point match (which happens if Black doesn’t double and White pulls the game out.)
Part (1) is pretty easy. White only wins if Black first doesn’t bear off his three checkers, which happens 31/36 of the time (note that 1-1 is not a winning double for Black), and White then rolls a double, which happens 1/6 of the time.
31/36 * 1/6 = 31/216 = 14.4%
[You might ask, “How do players actually do these calculations over the board?” I use a lot of numerical tricks, as do most other players. After you’ve played a lot of tournament backgammon, you realize that some tricks are particularly useful and some numbers recur constantly. In this calculation, I’d note that 31/36 is only a little larger than 5/6, so what’s 5/6 times 1/6? Well, 1/6 is about 16.7%, so 5/6 of that will be a little less than 14%. We want a number a little bigger than that, so our answer is 14%+. That’s plenty good enough for our purposes. Trying to get exact answers in your head is pretty hard, but close approximations are much easier and almost always good enough.]
What about part (2), the value of a 6-0 lead in a 7-point match? Since the Crawford Rule is in effect, White must win the next game, taking him to a 6-1 deficit. (It doesn’t matter if he wins a gammon in the Crawford Game or not.) He’ll then double to 2 at the start of every game. If he then never wins a gammon, he’ll need to win three more games to win the match, for a total of four straight wins overall. The probability of four straight wins between two equal players is
½ * ½ * ½ * ½ = 6.25%
But if White wins a gammon in either the second or third game, he wins 4 points and saves a game, so in that case he only needs to win three straight. The probability of that is 12.5%.
The probability of winning the match is therefore between 6.25% and 12.5%, and a little closer to the lower number, since you’re not favored to win a gammon in a two-game sequence. A good approximation is 9% for White’s chances, and therefore 91% for Black’s chances.
Finally, for Part (3) we need the value of leading 4-2 in a 7-point match. Different match equity tables give slightly different numbers here, but the range is roughly 64% to 66%. I’ll use 65% as a good average value.
Now we’re ready to figure out the optimal doubling and taking decisions at this score. Let’s start with White’s take/drop decision if he gets doubled.
> If White takes and redoubles to 8 when he can, he wins the match 14.4% of the time (from Part (1)).
> If White drops, he trails 0-6 to 7 and wins the match 9% of the time (Part (2)).
So if White gets doubled, he should take and reship when he can.
Now let’s look at Black’s doubling decision.
> If Black doubles, he must assume White takes and reships (we’re postulating correct play on both sides) so he’ll win the match 85.6% of the time.
> If Black doesn’t double, he’ll win this game 85.6%, getting to 6-0, and will lose 14.4%, getting to 4-2. His total winning chances then look like this:
85.6% of the time he’s leading 6-0, and wins 91% of those.
Wins in this variation = 85.6% * 91% = 77.9%.
14.4% of the time he’s leading 4-2, and wins 65% of those.
Wins in this variation = 14.4% * 65% = 9.4%.
Total wins from not doubling = 77.9% + 9.4% = 87.3%.
So he wins 87.3% if he doesn’t double, 85.6% if he does. So Black shouldn’t double, even in this two-roll position.
Now we’re ready to tackle the two main questions. What happens when we face real opponents of varying strengths?
(a) Against a very strong player (and assuming Black is a strong player himself) Black should just make the theoretically correct play and not double. If Black errs and doubles, White should take and redouble to 8 if Black misses.
(b) What about if Black is a strong player and is facing a weak opponent? This is a really interesting question and in fact is the whole point of this problem.
The theory of how to play against weak players originated in the 1970s with the publication of Barclay Cooke’s The Cruelest Game. Cooke expanded on his notions in two later books, Paradoxes and Probabilities and Championship Backgammon. Cooke’s idea was that you should be very conservative with the cube against weak players, doubling only when you were pretty sure you’d get a pass, and aiming to grind them down in a long series of 1-point and 2-point games, giving your huge skill advantage in checker play the maximum chance to work. The worst possible disaster was to give your weak opponent the cube in a volatile position, allowing him to rewhip to 4, win an 8-point gammon, and turn the match around.
Cooke was a well-liked fellow, a real gentleman of the old school. In addition, he was an absolutely superb writer, who was able to convey better than anyone else the glamour and excitement of high-level backgammon. The Cruelest Game, published in 1975, was one of the big influences driving the backgammon explosion of the mid-1970s. To this day, it remains the one book I would recommend if a friend who didn’t know the game came to me and wanted to understand why backgammon was popular and what the fuss was all about. Cooke captured the drama of the game better than anyone else, before or since.
Cooke’s ultra-conservative approach to playing weak players soon became accepted wisdom and was echoed in other books in the 1970s and 1980s. But it is, I think, completely the wrong approach. Let’s see why.
In Greek mythology, the gryphon was a majestic creature combining some disparate parts: the body of a lion with the wings of an eagle. Cooke’s “weak player” is a little like that: a hybrid containing components not likely to be found in nature. He plays the checkers so poorly that you’re a huge favorite to grind him down, one or two points at a time. But he handles doubling decisions superbly; he scoops up cubes in volatile but takeable positions that might have a strong player scratching his head, then he whips it back when the game starts to turn in his favor, applying maximum pressure. What a tiger!
Do real “weak players” actually play like this? In my experience, almost none do. In the real world, bad players handle the checkers poorly, but they handle the cube even worse. Their cube action is mostly tentative; they know they don’t play well, so they try to postpone decisions that might make them look foolish. They double late, or not at all, because they’re waiting for positions that are so strong that doubling can’t be a mistake. When doubled, they’d rather drop than take, because dropping only loses a point, while taking might lose four points. Besides, they know you’re a better player, and they’re picking up cues from you. If you’re doubling, then you must believe you have a big advantage. Who are they to argue? Better to drop.
The best way to play against weak players is to be very aggressive. Double a little early, especially in volatile positions. They’ll probably drop, but if they take, you’re better off in a number of ways:
> Their checker errors will now be occurring with the cube on 2 rather than 1.
> They may redouble prematurely, giving you an extra edge.
> They may redouble late or not at all, giving you a huge edge.
All of these edges add up to huge vigorish over time.
Interestingly, poker players tend to handle weak opponents better than backgammon players do. Poker players understand the value of relentless aggression, and they apply it ruthlessly, raising their limps, 3-betting their raises, and pushing the action after the flop. In part, I think, this is because poker players don’t really attach much importance to individual hands; there are many more hands in a poker session than games in a backgammon session, so poker players find it easier to just make what their experience tells them is the best move against this particular opponent, and let the chips fall where they may (pun intended).
Now, after this long intermezzo, back to Part (b). What do we do if we’re a strong player and our opponent is a weak player?
We double, and we do so quickly, without giving any hint that there might be something to think about. Our opponent will drop, because it’s a two-roll position, and everybody knows that’s a pass. And we pocket our two points and our 91-9 edge without risking losing the game.






